ETC/オムニホイール

先日、オムニホイールという車輪デバイスを見つけました。車輪の外輪に更に車輪がある不思議な形状をしています。

関連のサイトを調べているうちにどうしても手にとって見たくなり、土佐電子さんで販売しているTYPE2571を入手しました。

どんな風に使ったもんかと考え中。その思考過程のメモ。

目次

写真

図1
外見はこんな感じ。 矢印の方向が車輪の回転方向です。

図2
真ん中から２つに割れます。同じ形状の部品を互い違いに組み合わせられています。

この灰色のタル上の部分がフリーで回転します。車輪の回転方向に対して直角の力を空回り（キャンセル）することがミソのようです。

仮定

図3

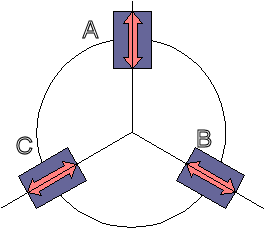図3は円盤状のシャーシに３つの駆動輪を配置して上から見た図。矢印が車輪の回転方向を意味します。それぞれのモータの出力をバランス良く制御すればどの方向にも進めるんじゃないか、それをどうやって実現するか、という話。

図4	図5

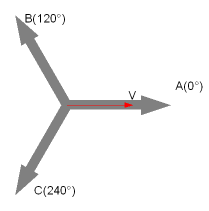
例えば、図4において赤矢印Vの方向へ移動したいとする。

• AとVの相関： cos(0-0) = 1
• BとVの相関： cos(0-120) = -0.5
• CとVの相関： cos(0-240) = -0.5

※ 負は逆回転を表す

相関はどれだけ関係が深いかを表す数値で、+1〜-1までの値を持つ。0が無関係を意味する。

つまりVの方向への移動に対し、Aの回転は100％の影響力を持ち、BとCは50％の影響力を持つことになる。

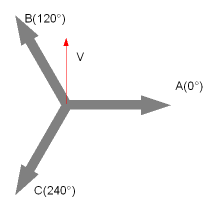
また図5において、赤矢印Vの方向へ移動したいとすると

• AとVの相関： cos(90-0) = 0
• BとVの相関： cos(90-120) = √3 ÷ 2 ≒ 0.87
• CとVの相関： cos(90-240) = -√3 ÷ 2 ≒ -0.87

Aは全く意味を成せず、BとCは約87％ほど影響力を持つことになる。

この相関値を利用すれば、任意の方向へ移動するのに必要な各駆動輪の速度が求められるんじゃないか。

試しに計算してみる

図6

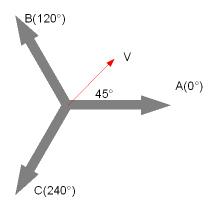45度の方向へ10[cm/s]で移動したい時。

• A-Vの相関値 = cos(45-0) ≒ 0.71
• B-Vの相関値 = cos(45-120) ≒ 0.26
• C-Vの相関値 = cos(45-240) ≒ -0.97

相関値から、

• Aの出力 10[cm/s] × cos(45) = 7.1[cm/s]
• Bの出力 10[cm/s] × cos(-75) = 2.6[cm/s]
• Cの出力 10[cm/s] × cos(-195) = -9.7[cm/s]

図7

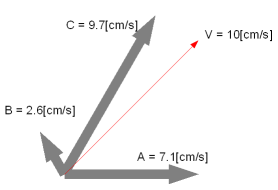速度と方向を矢印の長さと向きで表したのがこの図7。つまりこのような速度配分で駆動すれば、求める方向・速度で移動できるのではないか、と推測。

これで合ってるのかな。出来ると言えば出来るような気がするが。頭の中でシミュレーションしきれない俺、マジ頭悪い。実物で確認するしかないのか。

続く。