賭け事をする際、勝率が分かってる場合に効率よく財産を増やすためには、全財産のうちいくら賭けるべきかを与える公式があります。数学者のJ・L・ケリーさんが発表した公式で、ケリー基準とかオプティマルfとか呼ばれているらしいです。
本格的な解説や証明は他サイトに譲ることにして、使い方を忘れないようにメモ。
目次
公式
勝率をP、勝った時の報酬を掛け金のR倍とすると、最適な賭け金の割合fは次式で表される。
f = ((R + 1) * P - 1) / R
このfが0以下の場合は賭けに参加すべきではない。
逆に0より大きい場合は手持ちのお金のf倍を賭ける。グラフにするとこんな感じ。
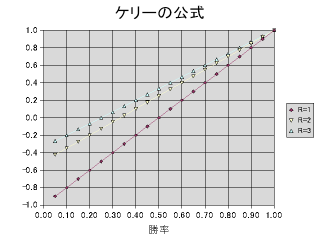 |
ケース1
問題
勝てば掛け金と同額がもらえ、負ければ掛け金を没収というギャンブルがある。ギャンブルの勝率が70%の時に、所持金1000円のうちいくら賭けるのが一番効率よく財産を増やせるか。
解答
勝率は70%なのでP=0.7、勝った時の報酬は掛け金と同額なのでR=1となる。これを当てはめると、
f = ((1 + 1) * 0.7 - 1) / 1 = 0.4
となる。つまり1000円の0.4倍、400円賭けることが最適となる。
ケース2
株のような負けても没収というわけじゃないケースはどうなるでしょうか。
問題
ある銘柄の価格が1000円の時に購入。200円上がるか100円下げたら終わり、という売買をする。勝率は50%。10万円持ってるとして何株買うのがベストか。
解答
実際は勝率なんか分からないのですけど、例えば過去のデータから統計的に確率が求められたと仮定。
この場合、利益と損失の比で考える。200円:100円なのでR=2、勝率50%なのでP=0.5となる。公式に当てはめて、
f = ((2 + 1) * 0.5 - 1) / 2 = 0.25
所持金10万の0.25倍、25000円を賭ける・・・となるが、このケースの場合負けても全額没収されるわけではない点に注意。
逆に25000円損するように買うと考える。100円下がって25000円、つまり250株買えということになる。
結論としては1000円を250株では25万円となり所持金をオーバーする。15万を借りて250株買うのも手ですが、とりあえず全力買いしろということですかね。